De la binouze au binaire
Des limites se font jour
L'ordinateur ne connait que le binaire
Si un programme doit conserver une valeur pendant sa session de travail, il va la garder dans la mémoire de l'ordinateur.
Le principe est exactement le même que pour les touches du clavier.
De plus, il lit toujours 8 bits d'un coup (un octet). Il ne tronque jamais.
Ainsi la valeur "3" qui nécessiterait uniquement 2 bits, le premier de valeur 1 et le second de valeur 2, est écrite sur un octet ce qui donne : 00000011.
Imaginez, si pour compter la valeur "3", vous utilisiez les doigts 1 et 2 et que l'on vous coupe les autres puisqu'ils ne sont pas utiles !
Avec un octet les valeurs sont limitées
La plus petite valeur que peut prendre un octet c'est zéro (0), aucun câble n'est allumé nous avons donc la valeur 0 en binaire soit : 00000000.

Figure 29 : Tous les bits sont éteints, l'octet est à 0.
La plus grande valeur que nous pouvons représenter sur un octet, c'est quand tous les câbles sont allumés, soit en binaire : 11111111.
Si le câble 1 est allumé nous avons la valeur 1. Mais si nous allumons aussi le second câble nous avons 2 + 1 = 3. Puis avec le troisième câble allumé, 4 + 2 + 1 = 7.
Si tous les câbles sont allumés, nous avons la valeur : 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255.

Figure 30 : Tous les bits sont utilisés, l'octet est à 255.
Notre programme doit conserver le calcul de 15 + 30 = 45.
Pour conserver la valeur 45, l'ordinateur utilisera 8 "cases" de mémoire. Il allumera les bits qui composent la valeur 45, c'est à dire le 1 (valeur 1), le 3 (valeur 4), le 4 (valeur 8) et le 6 (valeur 32).
Ce qui donne 32 + 8 + 4 + 1 = 45, et en représentation binaire :
00101101 (lecture de droite à gauche).
Utiliser plus d'octets
Mais qu’arrive-t-il si j'ai une valeur à conserver plus importante que les 255 possibles par exemple la valeur "767" ? Et bien la valeur sera stockée sur plus d'octets dans la mémoire.
Quand j'utilise 2 octets, je peux atteindre la valeur 65 535, ainsi pour stocker ma valeur, le système va utiliser non plus 8 bits mais 16 bits.
Pour la valeur "767", il va allumer toutes les"cases" (bits) du premier octet pour atteindre la valeur "255", et allumer sur le second octet les bits qui additionnés donne la valeur manquante.
Si je réalise le calcul entre mon nombre à stocker et la valeur du premier octet, 767 - 255, je trouve la valeur 512. J'allumerais les bits du second octet qui additionnés donnent la valeur 512.
Le premier bit du second octet prend la valeur 256, nous l'avons vu plus haut où j'ai demandé la valeur du neuvième câble, et bien on peut dire que le premier bit du second octet c'est le 9° câble.
Le second bit du deuxième octet, prend la valeur 512 (256 * 2). C'est justement la valeur qu'il nous faut trouver.
Il va donc allumer sur le second octet le second bit.

Figure 31 : Utilisation de plusieurs octets.
Dans cet exemple, 10 bits suffiraient pour conserver la valeur, mais non, le système utilise toujours un multiple de 8 bits, donc ici 16 bits (2 octets).
Si mon nombre est plus grand, il prendra 4 ou 16 ou plus d'octets.
Un autre exemple, un fichier
Si j'écris la lettre "b" dans un fichier texte. Sa valeur c'est le code ASCII "98" qui s'écrit "011000010" en binaire.
C'est cette valeur qui sera inscrite sur les pistes magnétiques du disque lors de l'enregistrement.
Pour conserver mon fichier sur le disque dur, j'ai besoin d'un octet (8 "cases" du disque dur).
Si j'écris le texte "bons jours", sur le disque j'ai une suite d'octets (un par caractère), ce qui donne :
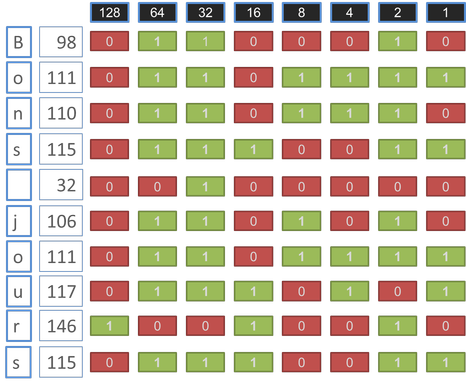
Figure 32 : Un fichier est une suite de bits.
Cette chaine est composée de 10 caractères (la touche espace est un caractère de code ASCII "32"), chaque caractère occupe 8 bits (1 octet), mon fichier sur le disque occupera 10 caractères (10 octets) * 8 bits = 80 bits (ou 80 "cases" sur le disque dur).
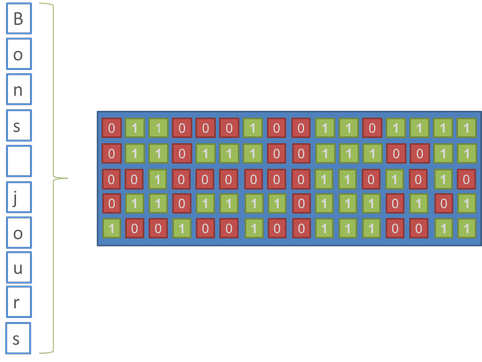
Figure 33 : Les bits du fichier sont écris dans des bits du support de stockage.
Des multiples de l'octet
Un fichier est rarement aussi petit que notre fichier texte. Une vidéo conserve un nombre important d'informations tout comme une image.
Au lieu de dire – Mon fichier fait 1 000 octets ou 8000 bits, nous dirons, – Mon fichier fait 1 Kilo-Octets (Ko).
S'il fait 1 million d'octets, nous dirons 1 Méga-Octet (Mo). Avec 1 milliard d'octets, nous aurons 1 Giga-Octets (Go).
Avec mille milliards d'octets (8 000 000 000 000 bits), c'est un téra-Octet (1 To).
Un fichier de 3 Ko, c'est 3 * 1000 (octets) * 8 (bits) soit 24 000 bits ou si vous préférez 24 000 "cases" du disque remplies de zéros et de uns.
32 bits ou 64 bits
J'ai un système 32 bits (4 octets), ce programme est compatible 64 bits (8 octets), cela veut dire quoi ?
C'est simplement la quantité d'informations que l'ordinateur est capable de traiter en 1 opération (un cycle d'horloge).
En 64 bits, il traite deux fois plus d'informations qu'en 32 bits.
Conclusion
Vous connaissant, je suis sûr que d'autres questions vous empêchent d'avoir une vie saine et équilibrée.
Et si j'ai des valeurs négatives, comment compter en binaire, et les opérateurs bits à bits, les rotations et décalages de bits (vous ne dormez donc jamais ?).
– Alors Muchmuch t'as compris cette fois ?
J'ai fait une expérience de retour dans le passé quand j'ai vu son regard, j'ai vu Archimède s'écriant Eureka !
Je vous propose un petit exercice sympathique.
Lisez le texte suivant (vous avez 8 secondes), éteignez l'écran ou tournez-le loin de votre regard.
Maintenant vous avez 64 secondes pour traduire le texte en binaire (pour la correction, attendez mon retour de vacances).
Les plus aguerris ferons la conversion de tête, les autres peuvent prendre un papier et un crayon.
Autrement dit
Le binaire est une façon de compter à la con avec des uns et des zéros qui veulent dire que t'es là ou que t'es pas là.
Pour compter tu vas utiliser 8 doigts alors que le bon dieu t'en a donné 10, ainsi cela nous éclaire sur son inventeur, j'en déduis qu'il lui manquait deux doigts.
Pour simplifier les choses, ton premier doigt il vaut un (après réflexion, cela me semble correct), le deuxième doigt vaut naturellement 2 (jusque-là je n'ai rien à dire), mais le 3° doigt prend la valeur 4 et le 4° la valeur 8
– alors là je dis stop ! Vous exagérez –.
De plus, vous comptez de droite à gauche, étant Anglo-Saxon, l'ordinateur est culturellement dyslexisque.
L'ordinateur, c'est la seule langue qu'il connait, le lézard qui squatte mon balcon reconnait 3 cris différents, il est donc 1,5 fois plus intelligent que mon ordinateur, mais c'est vrai qu'il est 6000 % de fois moins rapide.
Si je veux compter de grands nombres, j'ai besoin de l'aide des amis car avec deux mains cela ne suffit pas, pour ceux qui sont seuls, ne vous inquiétez pas, pour compter votre salaire, vos deux mains suffiront.
Si vraiment vous avez beaucoup d'amis (mais trouver des amis avec 8 doigts n'est pas simple), vous pourrez garder beaucoup d'informations, vous pouvez avoir 1 kilo d'amis, 1 Méga d'amis, voire 1 Giga d'amis, rares sont les personnes avec un compte Facebook aussi actif.
Il ne sera pas facile de leur demander de garder les doigts ouverts, les mains en l'air. Remarquez qu'un bug peut se produire si un de vos amis pris d'une envie pressante s'absente temporairement.

